Serie de Fourier
Una serie de Fourier es una serie infinita que converge puntualmente a una función periódica y continua a trozos(o por partes). Las series de Fourier constituyen la herramienta matemática básica del análisis de Fourier empleado para analizar funciones periódicas a través de la descomposición de dicha función en una suma infinita de funciones senoidales mucho más simples (como combinación de senos y cosenos con frecuencias enteras). El nombre se debe al matemático francés Jean-Baptiste Joseph Fourier que desarrolló la teoría cuando estudiaba la ecuación del calor. Fue el primero que estudió tales series sistemáticamente, y publicando sus resultados iniciales en 1807 y 1811. Esta área de investigación se llama algunas veces Análisis armónico.
Las series de Fourier tienen la forma:
Donde  y
y 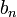 se denominan coeficientes de Fourier de la serie de Fourier de la función
se denominan coeficientes de Fourier de la serie de Fourier de la función 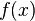
 y
y 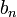 se denominan coeficientes de Fourier de la serie de Fourier de la función
se denominan coeficientes de Fourier de la serie de Fourier de la función 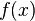
Ortogonalidad
Se puede usar la fórmula del sumatorio para probar una relación de ortogonalidad:
donde δ es la delta de Kronecker.
De lo anterior, las columnas de esta matriz son ortogonales y por tanto es unitaria. De hecho, esta matriz es precisamente la transformada de Fourier discreta (aunque varían la normalización y la convención de signos).
Las raíces n-ésimas de la unidad forman una representación irreducible de cualquier grupo cíclico de orden n. La relación de ortogonalidad se obtiene de los principios de teoría de grupos descritos en el grupo de caracteres.
Las raíces de la unidad aparecen en los autovectores de las matrices hermitianas (por ejemplo, de la laplaciana discretizada unidimensional con límites periódicos), de los que se obtiene también la propiedad de ortogonalidad (Stran, 1999).
Se dice que una función f es impar cuando para cualquier x en el dominio de f se tiene que f(-x)=-f(x). Modifica los valores de x en la escena y observa qué sucede con los valores de f(x) y de f(-x). Al ir modificando los valores de x la gráfica muestra también los valores de -x, de f(x) y de f(-x). Observa que para cualquier valor del dominio, f(x)=-f(x). Habrás notado además que el segmento que une los puntos P1 y P siempre pasa siempre por el origen, punto del cual equidistan. funcion par:
Ejemplos La función y(x)=x es impar ya que: f(-x) = -x pero como f(x) = x entonces: f(-x) = - f(x).  |
La función f(x)=x2 es par ya que f(-x) = (-x)2 =x2

![\frac{a_0}{2} + \sum_{n=1}^\infty\left[a_n\cos\frac{2n\pi}{T}t + b_n\sin\frac{2n\pi}{T}t\right]](http://upload.wikimedia.org/math/5/5/8/558025a943d5a46c353605d33c6b6d2c.png)

 cuyo elemento
cuyo elemento 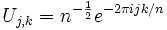
 .
.