RESOLVER LAS ECUACIONES UTILIZANDO
LAS TRANSFORMADAS DE LAPLACE
Problema 1.- 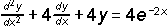 con las condiciones :
con las condiciones : 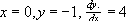
Paso 1.- Se aplica la transformada de Laplace a toda la ecuación término a término. 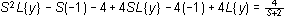
Paso 2.-- Sumando los términos semejantes 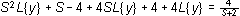
Paso 3.- Se factoriza la transformada : 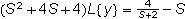
Paso 4.- Se despeja la transformada: 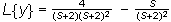
Paso 5.-- Se obtiene la transformada inversa de Laplace
Paso 6.- 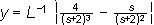
Paso 7.- Se obtiene el resultado final:
Resultado
La solución de la ecuación, puede obtenerse en el Mathematica con la instrucción: DSolve[{y'' [x]+4 y'[x]+4 y[x]==4 E^(-2 x),y[0]== -1,y'[0]==4},y[x],x]
Una gráfica de la solución es:
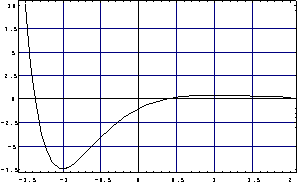
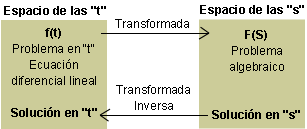
Se puede representar la actividad de la transformada de Laplace mediante el siguiente esquema: