En
matemática, la
transformada de Fourier es una
aplicación que hace corresponder a una función
f, con valores
complejos y definida en la recta, con otra función
g definida de la manera siguiente:
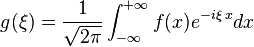
Donde
f es

, o sea
f tiene que ser una función
integrable en el sentido de la
integral de Lebesgue. El factor, que acompaña la integral en definición facilita el enunciado de algunos de los teoremas referentes a la transformada de Fourier. Aunque esta forma de normalizar la transformada de Fourier es la más comúnmente adoptada, no es universal. En la práctica las variables x y
ξ suelen estar asociadas a dimensiones (como el espacio -metros-, frecuencia -segundos^-1-,...) y entonces es correcto utilizar la fórmula alternativa:

de forma que la constante beta cancela la dimensiones asociadas a las variables obteniendo un exponente adimensional.
La transformada de Fourier así definida goza de una serie de propiedades de continuidad que garantizan que puede extenderse a espacios de funciones mayores e incluso a espacios de
funciones generalizadas.
Además, tiene una multitud de aplicaciones en muchas áreas de la ciencia e ingeniería: la
física, la
teoría de los números, la
combinatoria, el
procesamiento de señales (electrónica), la
teoría de la probabilidad, la
estadística, la
óptica, la
propagación de ondas y otras áreas. En procesamiento de señales la transformada de Fourier suele considerarse como la decomposición de una señal en componentes de
frecuencias diferentes, es decir,
g corresponde al
espectro de frecuencias de la señal
f.
La rama de la matemática que estudia la transformada de Fourier y sus generalizaciones es denominada
análisis armónico.
Son varias las notaciones que se utilizan para la transformada de Fourier de f. He aquí algunas de ellas:
![\mathcal{F}[f], \hat f, F(f), \mathcal{F} \{ f \}](http://upload.wikimedia.org/math/2/d/6/2d64cf82c8d2c146759492918c64336d.png) .
.
Transformada Z
En las
matemáticas y
procesamiento de señales, la
Transformada Z convierte una
señal real o
compleja definida en el
dominio del tiempo discreto en una representación en el
dominio de la frecuencia compleja.
El nombre de Transformada Z procede de la
variable del
dominio, al igual que se podría llamar "Transformada S" a la
Transformada de Laplace. Un nombre más adecuado para la TZ podría haber sido "Transformada de Laurent", ya que está basada en la
serie de Laurent. La TZ es a las señales de tiempo discreto lo mismo que Laplace a las señales de tiempo continuo.
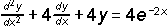 con las condiciones :
con las condiciones : 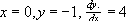
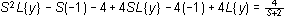
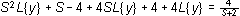
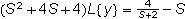
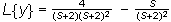
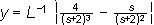
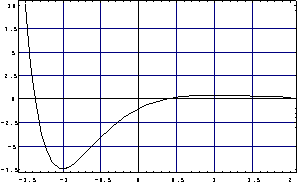
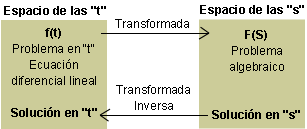
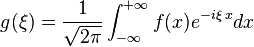
 , o sea f tiene que ser una función
, o sea f tiene que ser una función 
![\mathcal{F}[f], \hat f, F(f), \mathcal{F} \{ f \}](http://upload.wikimedia.org/math/2/d/6/2d64cf82c8d2c146759492918c64336d.png) .
.![\frac{a_0}{2} + \sum_{n=1}^\infty\left[a_n\cos\frac{2n\pi}{T}t + b_n\sin\frac{2n\pi}{T}t\right]](http://upload.wikimedia.org/math/5/5/8/558025a943d5a46c353605d33c6b6d2c.png)
 y
y 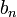 se denominan coeficientes de Fourier de la serie de Fourier de la función
se denominan coeficientes de Fourier de la serie de Fourier de la función 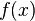

 cuyo elemento
cuyo elemento 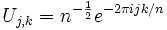
 .
.


 es la
es la 










 representa la
representa la 



 , la transformada de Laplace de f(t) se define como
, la transformada de Laplace de f(t) se define como