Unidad III: Definicion de transformada de Laplace. linealidad. propiedades de la transformada de Laplace.

                        Definición de la Transformada

Sea f una función definida para , la transformada de Laplace de f(t) se define como

cuando tal integral converge
Notas

1. La letra s representa una nueva variable, que para el proceso de integracion se considera constante
2. La transformada de Laplace convierte una funcion en t en una funcion en la variable s
3. Condiciones para la existencia de la transformada de una función:
   1. De orden exponencial
   2. Continua a trozos

Linealidad

                Propiedades de la Transformada

En las siguientes propiedades se asume que las funciones f(t) y g(t) con funciones que poseen transformada de Laplace.
Las demostraciones pueden ser obtenidas en el libro de Zill: A first course in Differential Equations with modelling applications

1. Linealidad (Ejemplos, Demostracion,
   
   

   Idea
   La transformada de Laplace se distribuye sobre las sumas o restas y saca constantes que multiplican.

   
   Versión para la inversa:
   
   
2. Primer Teorema de Traslación (Ejemplos, Demostracion,
   
   donde
   
   

   Idea
   La transformada de Laplace se convierte un factor exponencial en una traslación en la variable s.
   

   Versión para la inversa:
   
   
3. Teorema de la transformada de la derivada (Ejemplos, Demostracion, 
   

   Idea
   La transformada de Laplace cancela la derivada multiplicando por la variable s.

   
   
4. Teorema de la transformada de la integral (Ejemplos
   
   
   
5. Teorema de la integral de la transformada (Ejemplos
   
   Siempre y cuando exista
   
   
   
6. Teorema de la derivada de la transformada (Ejemplos
   
   
   
7. Transformada de la función escalón (Ejemplos
   

   Si representa la función escalón unitario entonces
   
   
   

8. Segundo teorema de Traslación (Ejemplos
   
   
   
9. Transformada de una función periódica
   

   Si f(t) es una función periódica con período T:
   
   

Teorema de la Convolución
Si f * g representa la convolución entre las funciones f y g entonces
 

 Ejercicios:

TRANSFORMADAS DE LAPLACE POR DEFINICIÓN:

 1.

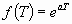
L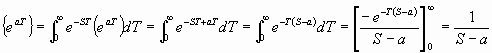

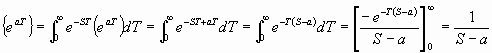
2.

L