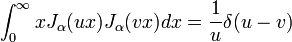Ecuacion de Cauchy-Riemam
Las condiciones de Cauchy-Riemann son básicas en el Análisis Complejo, debido a que su verificación constituye una condición necesaria para la derivabilidad de este tipo de funciones.
Sea una función compleja f(z), con z = x + iy y f(z) se puede descomponer en suma de dos funciones reales de dos variables u y v, de manera que f(z) = f(x,y) = f(x + iy) = u(x,y) + iv(x,y). Si la función f(z) sea derivable en un punto z0 = x0 + iy0 entonces deben verificarse las condiciones de Cauchy-Riemann:
Además se cumple que el valor de la derivada en el punto, de existir, debe ser:
ten formas equivalentes de expresar las condiciones de Cauchy-Riemann:

Sin embargo, existen condiciones suficientes de derivabilidad si la función, además de cumplir las ecuaciones de Cauchy-Riemann, se puede descomponer en dos funciones u y v con derivadas parciales primeras continuas en un entorno de z0 = (x0,y0).
Funcion Gamma-propiedades.
Aplicaciones de la función Gamma
Cálculo fraccionario:
La n-ésima derivada de axb (donde n es un número natural) se puede ver de la siguiente manera:
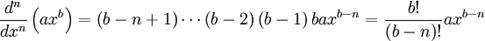
como n! = G(n + 1) entonces 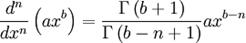 donde n puede ser cualquier número donde gamma esté definido o se pueda definir mediante límites.
donde n puede ser cualquier número donde gamma esté definido o se pueda definir mediante límites.
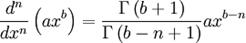 donde n puede ser cualquier número donde gamma esté definido o se pueda definir mediante límites.
donde n puede ser cualquier número donde gamma esté definido o se pueda definir mediante límites.De esta manera se puede calcular por ejemplo, la 1/2 derivada de x, de x2 e inclusive de una constante c = cx0:
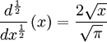
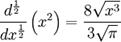
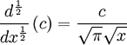
Propiedades:
De la representación integral se obtiene:
 .
.
Otras ecuaciones funcionales importantes de la función Gamma son la fórmula de reflexión de Euler
y la fórmula de duplicación
La fórmula de duplicación es un caso especial del teorema de multiplicación
Una propiedad básica y muy útil de la función Gamma , que puede obtenerse a partir de la definición mediante productos infinitos de Euler es:
Quizá el valor más conocido de la función Gamma con argumento no negativo es
La cual puede obtenerse haciendo z = 1 / 2 en la fórmula de reflexión o en la fórmula de duplicación, usando la relación de la función Gamma con la función beta dada más abajo con x = y = 1 / 2 o haciendo la sustitución  en la definición integral de la función Gamma, con lo que se obtiene una integral Gaussiana. En general, para valores impares de n se tiene:
en la definición integral de la función Gamma, con lo que se obtiene una integral Gaussiana. En general, para valores impares de n se tiene:
 en la definición integral de la función Gamma, con lo que se obtiene una integral Gaussiana. En general, para valores impares de n se tiene:
en la definición integral de la función Gamma, con lo que se obtiene una integral Gaussiana. En general, para valores impares de n se tiene: (n impar)
(n impar)
donde n!! denota al doble factorial.
Las derivadas de la función Gamma vienen dadas por la función poligamma. Por ejemplo:
La función Gamma tiene un polo de orden 1 en z = − n para todo número natural y el cero. El residuo en cada polo es:
El teorema de Bohr-Mollerup dice que, entre todas las funciones que generalizan el factorial de los números naturales a los reales, sólo la función Gamma es logaritmo convexa (o log-convexa), esto es, el logaritmo natural de la función Gamma es una función convexa.
El desarrollo en Serie de Laurent de Γ(z) para valores 0 < z < 1 es:
Donde ζ(n) es la función zeta de Riemann.
Valores de la función Gamma
Función de Bessel
Las funciones de Bessel o funciones cilíndricas, se utilizan en la mecánica gravitatoria, pero también se aplican en otros campos como la propagación de ondas electromagnéticas y de calor. Las funciones de Bessel aparecen como coeficientes en las series de expansión de la perturbación indirecta de un planeta causada por el movimiento del Sol.
aplicaciones
La Ecuación de Bessel aparece cuando se buscan soluciones a la ecuación de Laplace o a la ecuación de Helmholtz por el método de separación de variables en coordenadas cilíndricas o esféricas. Por ello, las funciones de Bessel son especialmente importantes en muchos problemas de propagación de ondas, potenciales estáticos y cualquier otro problema descrito por las ecuaciones de Helmholtz o Laplace en simetrías cilíndricas o esféricas. Cuando se resuelven sistemas en coordenadas cilíndricas, se obtienen funciones de Bessel de orden entero (α = n) y en problemas resueltos en coordenadas esféricas, se obtienen funciones de Bessel de orden semientero (α = n + 1 / 2), por ejemplo:
- Ondas electromagnéticas en guías de onda cilíndricas.
- Modos transversales electromagnéticos en guías ópticas.
- Conducción del calor en objetos cilíndricos.
- Modos de vibración de una membrana delgada circular (o con forma de anillo).
- Difusión en una red.
También se usan funciones de Bessel en otro tipo de problemas como en procesado de señales.
Integrales de Bessel
Para valores enteros de n, se tiene la siguiente representación integral:
Que también se puede escribir como:
Esta es la aproximación usada por Bessel en su estudio de estas funciones, y a partir de esta definicion dedujo varias propiedades de las mismas. Esta definición integral puede extenderse a órdenes no enteros añadiendo otro término integral:
también se tiene, para 

Propiedades
Para enteros de orden α = n, Jn(x) se puede definir a partir de la serie de Laurent de la siguiente función generatriz:
aproximación tomada por P. A. Hansen en 1843. Esta expresión puede generalizarse a órdenes no enteros usando integración de contorno u otros métodos. Otra expresión importante para órdenes enteros es la identidad de Jacobi-Anger:
identidad que es usada para expandir ondas planas en una serie infinita de ondas cilíndricas o para encontrar la serie de Fourier de un tono de una señal de FM.
Más generalmente, una función ƒ se puede expandir en una serie de la forma
que se denomina expansión de Neumann de ƒ. Los coeficientes de esta serie en el caso ν = 0 tienen la siguiente forma explícita
donde Ok son los polinomios de Neumann.
Existen funciones que admiten la siguiente representación especial
con
debido a la rtelación de ortogonalidad

Más generalmente, si f tiene un punto de ramificación donde
| f(z) = | ∑ | akJν + k(z), |
| k = 0 |
entonces

- o

Otra manera de definir las funciones de Bessel son la representación de Poisson y la fórmula de Mehler-Sonine:
donde ν > −1/2 y z es un número complejo Esta fórmula es especialmente útil cuando se trabaja con transformadas de Fourier.
Donde Z denota J, Y, H(1), o H(2).
Estas dos identidades se suelen combinar para obtener otras relaciones distintas. Por ejemplo, se pueden calcular funciones de Bessel de mayores órdenes (o mayores derivadas) a partir de funciones de Bessel de menor orden o de derivadas de menor orden. En particular, se cumple:
Las funciones modificadas de Bessel cumplen relaciones similares:
Las relaciones de recurrencia serán en este caso:
donde Cα denotará a Iα o a eαπiKα. Estas relaciones son útiles para problemas de difusión discreta.
La división de la ecuación de Bessel por x es una ecuación hermítica o auto-adjunta, por lo que sus solucciones deben cumplir determinadas relaciones de ortogonalidad para unas condiciones de contorno adecuadas. En particular, se cumple:
donde α > − 1, δn,m es la delta de Kronecker, y uα,m es el m-ésimo cero de Jα(x). Esta relación de ortogonalidad puede ser usada para extraer coeficientes de las series de Fourier-Bessel, donde una función se expande en una base de funciones de Bessel Jα(xuα,m) para α fijo y m variable. (Obtener una relación análoga para funciones de Bessel esféricas es trivial.)
Se puede obtener de forma inmediata una relación análoga para funciones de Bessel esféricas:
Otra relación de ortogonalidad es la ecuación de cierre:
para α > − 1 / 2 y siendo δ(x) la función delta de Dirac. Esta propiedad se usa para construir expansiones de funciones arbitrarias como series de funciones de Bessel mediante la transformada de Hankel.
Para funciones de Bessel esféricas, la relación de cierre es:
para α > − 1. Otra propiedad importante de la ecuación de Bessel, que se deriva de la identidad de Abel, es el Wronskiano de las soluciones:
donde Aα y Bα son dos soluciones cualesquiera independientes de la ecuación de Bessel y Cα es una constante independiente de x (que depende de α y de las funciones de Bessel consideradas). Por ejemplo, se cumple:
Existe un gran número de integrales e identidades que involucran a funciones de Bessel que no están aquí reproducidas, pero que se pueden encontrar en las referencias.

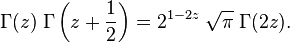




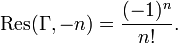
![\Gamma(z) \approx \frac{1}{z} -\gamma +
\left[\frac{\gamma^2}{2!}+ \frac{\zeta(2)}{2} \right]x+
\left[\frac{\gamma^3}{3!}+ \frac{\zeta(2)}{2}\gamma+ \frac{\zeta(3)}{3} \right]x^2+
\dots](http://upload.wikimedia.org/math/0/1/2/012da0b2a6233ee13452295c6fb63db1.png)
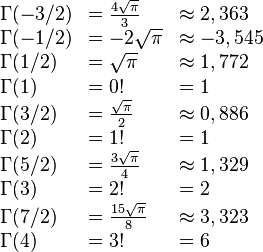






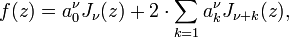


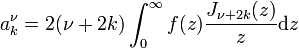
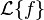 es la
es la 
 y
y 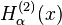 cumplen las siguientes
cumplen las siguientes 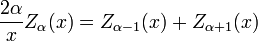

![\left( \frac{d}{x dx} \right)^m \left[ x^\alpha Z_{\alpha} (x) \right] = x^{\alpha - m} Z_{\alpha - m} (x)](http://upload.wikimedia.org/math/d/1/a/d1a58356b3bf0462c7c606ccac45de73.png)
![\left( \frac{d}{x dx} \right)^m \left[ \frac{Z_\alpha (x)}{x^\alpha} \right] = (-1)^m \frac{Z_{\alpha + m} (x)}{x^{\alpha + m}}](http://upload.wikimedia.org/math/9/d/5/9d5dd962bc4994f8c33dee1a746b7488.png)
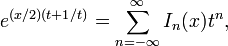

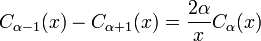

![\int_0^1 x J_\alpha(x u_{\alpha,m}) J_\alpha(x u_{\alpha,n}) dx
= \frac{\delta_{m,n}}{2} [J_{\alpha+1}(u_{\alpha,m})]^2
= \frac{\delta_{m,n}}{2} [J_{\alpha}'(u_{\alpha,m})]^2,](http://upload.wikimedia.org/math/f/3/e/f3e279f4113b9b3a4ec460a4fc215fe7.png)
![\int_0^1 x^2 j_\alpha(x u_{\alpha,m}) j_\alpha(x u_{\alpha,n}) dx = \frac{\delta_{m,n}}{2} [j_{\alpha+1}(u_{\alpha,m})]^2](http://upload.wikimedia.org/math/f/8/1/f8170c68df8d90616bdab542dc33f33a.png)