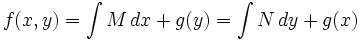Bienvenidos

BIENVENIDOS A MI BLOG
            Ecuaciones diferenciales exacta 
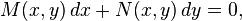
M(x, y)\, dx + N(x, y)\, dy = 0, \,\! 
en donde las derivadas parciales de las funciones M y N: \frac{\partial M}{\partial y} \,\! y \frac{\partial N}{\partial x} \,\! son iguales. Esto es equivalente a decir que existe una función F(x,y)=0 tal que

dF(x,y)=\frac{\partial F}{\partial x}dx+\frac{\partial F}{\partial y}dy \,\!
donde \frac{\partial F}{\partial x}=M(x,y)\,\! y \frac{\partial F}{\partial y}=N(x,y)\,\!. Dado que F(x,y) es una función diferenciable entonces las derivadas cruzadas deben ser iguales y esta es la condición \frac{\partial M}{\partial y}=\frac{\partial N}{\partial x}= \frac{\partial^2 F}{\partial x \partial y} \,\!.

                                                     Método de resolución.

Para resolver una ecuación diferencial de este tipo, se ha de seguir los siguientes pasos:
  • Comprobar la exactitud de la ecuación, esto es, verificar si las derivadas parciales de M (con respecto a y) y de N (con respecto a x) son iguales.
  • Se integra M o N a conveniencia (M respecto a x o N respecto a y) obteniéndose de este modo la solución general de la ecuación aunque con una función incógnita g que aparece como constante de integración. Esto es:
f(x,y) = \int M\,dx + g(y) = \int N\,dy + g(x) \,\!
  • Para despejar la función g se deriva 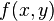f(x,y)\,\! con respecto a la variable independiente de g.
  • Se iguala g' con M o N (si se integró M se iguala a N y viceversa.), despejando y luego integrando con respecto a la variable dependiente de g; de este modo se encontrará la función g.
  • Finalmente se reemplaza el g encontrado en la solución general f(x,y)\,\!.
  •  
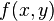EJEMPLOS RESUELTOS DE ECUACIONES DIFERENCIALES EXACTAS
 
sea la función diferencial:

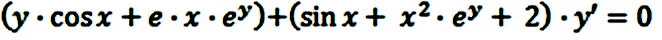
ecuaciones diferenciales

Solución

Para ver que esta ecuación diferencial es de diferenciales exactas hacemos:

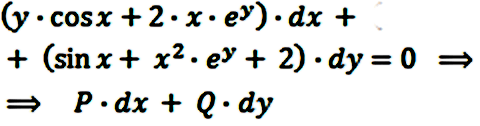
ecuaciones diferenciales

Y tenemos:

ecuaciones diferenciales

Siendo cierto que la ecuación es del tipo de diferenciales exactas, podemos calcular con facilidad la función integral:

ecuaciones diferenciales

Para conocer el valor de la función derivamos U(x, y) respecto de y, e igualamos el resultado a Q:

ecuaciones diferenciales

Así pues, la solución general de la ecuación diferencial estudiada será:

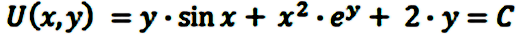
ecuaciones diferenciales

ejercicios:

sea la función diferencial:

ecuaciones diferenciales

Solución.

Operando como en los casos anteriores se comprueba que esta ecuación no es una ecuación diferencial exacta, no obstante, si multiplicamos todos los términos por 1/xy2 nos queda:

ecuaciones diferenciales

Con lo que obtenemos una ecuación diferencial que si cumple las condiciones de ser diferencial exacta y a la que podemos aplicarle el método que estamos desarrollando:

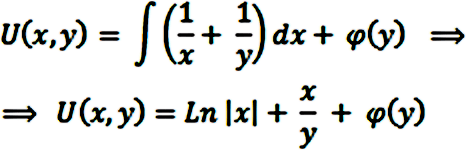
ecuaciones diferenciales

Derivando respecto de y e igualando a Q:

ecuaciones diferenciales

Y de esa forma, la solución general será:

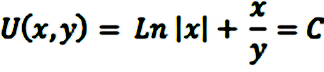
ecuaciones diferenciales

Que es válida para todos los puntos en los que se cumpla que x e y son distintos de 0.

Aparte de la solución general, podemos ver que existe una solución singular para el caso y = 0 ó x = 0 ya que entonces la ecuación se verifica trivialmente.

El término 1/xy2 recibe el nombre de factor integrante y resulta fácil comprobar que, en general, introduce soluciones singulares en los casos en los que se opera con él. 
Publicado por en