Una ecuación diferencial (ED) es una ecuación que relaciona de manera no trivial a una función desconocida y una o más derivadas de esta función desconocida con respecto a una o más variables independientes. Si la función desconocida depende de una sola variable la ecuación diferencial se llama ordinaria , por el contrario, si depende de más de una variable, se llama parcial .
La frase de manera no trivial que hemos usado en la definición anterior tiene como propósito descartar ecuaciones diferenciales que satisfacen la definición, pero son realmente identidades, es decir, son siempre verdaderas sin importar quién sea la función desconocida. Un ejemplo de tal tipo de ecuaciones es:
Ejemplo
La ecuación es equivalente a las dos ecuaciones diferenciales
es equivalente a las dos ecuaciones diferenciales
La ecuación
Las ecuaciones diferenciales se clasifican en varias categorías, como ya vimos, según su tipo en ordinarias y parciales, o según su linealidad u orden, como veremos.
Ejemplo
La ecuación diferencial
La ecuación diferencial
es de primer orden, no lineal y no homogénea. Esta ecuación surge en sicología y representa un modelo del aprendizaje. La variable  representa el nivel de habilidad del individuo como una función del tiempo
representa el nivel de habilidad del individuo como una función del tiempo  . Las constantes
. Las constantes  y
y  dependen del individuo considerado y de la naturaleza de la tarea que se este aprendiendo.
dependen del individuo considerado y de la naturaleza de la tarea que se este aprendiendo.
Ejemplo
La ecuación
La ecuación
es de segundo orden, lineal con coeficientes constantes y no homogénea. Esta ecuación diferencial surge en el estudio de circuitos eléctricos que consisten de un inductor  , un resistor
, un resistor  y un capacitor
y un capacitor  , al cual se aplica una fuerza electromotriz
, al cual se aplica una fuerza electromotriz  .
.
Ejemplo
La ecuación
La ecuación
es de orden 3, lineal con coeficientes constantes y homogénea.
La ecuación
es de primer orden, no lineal y no homogénea.
La ecuación
es de segundo orden, lineal con coeficientes variables y no homogénea.
ejencicio:
Tenemos una ecuación diferencial lineal puesto que es de la forma:
P0(x)·y’ + P1(x)·y = R(x)Por teoría sabemos que la ecuación es diferencial exacta si cumple P’0 = P1. Como en este caso no ocurre así buscamos un factor integrante:
Y a partir de ahí tenemos:
ejercicios propuestos:
Resolver la ecuación diferencial :
y' = p(x).y = 0con la condición y(0) = 1 siendo :

Resolver la ecuación diferencial :


Resolver la ecuación diferencial :


Resolver la ecuación diferencial :


Resolver la siguiente ecuación :
y' = (x + y)con la condición y(0) = 1.
Resolver la siguiente ecuación diferencial :


POR ORDEN
El orden de la derivada mayor que existe en la ec. Diferencial, entiendase por orden a la cantidad de veces que se deriva una funcion ejemplo:
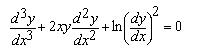 el orden es 3 puesto que la mayor de las derivadas es y“`.
el orden es 3 puesto que la mayor de las derivadas es y“`. POR GRADO
Es el grado de la derivada de mayor orden que existe en la ecuacion diferencial.Entiendase por grado la potencia a la que esta elevada la derivada. ejemplo:
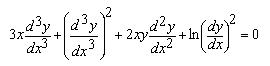 el grado de esta ecs. es 2 ya que y“` esta elevada ala segunda
el grado de esta ecs. es 2 ya que y“` esta elevada ala segunda potencia.
Tipo de solución de una ecuación diferencial
Tipos de soluciones
Una solución de una ecuación diferencial es una función que al reemplazar a la función incógnita, en cada caso con las derivaciones correspondientes, verifica la ecuación, es decir, la convierte en una identidad. Hay tres tipos de soluciones:
- Solución general: una solución de tipo genérico, expresada con una o más constantes. La solución general es un haz de curvas. Tiene un orden de infinitud de acuerdo a su cantidad de constantes (una constante corresponde a una familia simplemente infinita, dos constantes a una familia doblemente infinita, etc). En caso de que la ecuación sea lineal, la solución general se logra como combinación lineal de las soluciones (tantas como el orden de la ecuación) de la ecuación homogénea (que resulta de hacer el término no dependiente de y(x) ni de sus derivadas igual a 0) más una solución particular de la ecuación completa.
- Solución particular: Si fijando cualquier punto P(X0,Y0) por donde debe pasar necesariamente la solución de la ecuación diferencial, existe un único valor de C, y por lo tanto de la curva integral que satisface la ecuación, éste recibirá el nombre de solución particular de la ecuación en el punto P(X0,Y0), que recibe el nombre de condición inicial. Es un caso particular de la solución general, en donde la constante (o constantes) recibe un valor específico.
- Solución singular: una función que verifica la ecuación, pero que no se obtiene particularizando la solución general.
Verificacion de la solucion de una E.D
Demostrar que
Es una solución de la ecuación diferencial
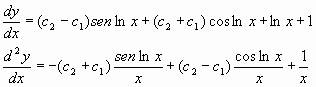
Sustituyendo los valores en la ecuación diferencial original encontramos que la relación de variables satisface la ecuación
Demostrar que
Es una solución particular de la ecuación diferencial
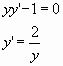
Sustituyendo el valor y’ en la ecuación diferencial y reduciendo obtenemos
ejercicios propuestos:
Verifica las soluciones de las siguientes ecuaciones diferenciales