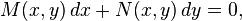Bienvenidos

BIENVENIDOS A MI BLOG

Ecuaciones diferenciales ordinarias de primer orden

                                     Ecuaciones diferenciales ordinarias de primer orden

Una ecuación diferencial de primer orden con la condición inicial se expresa de la siguiente forma:
[L] = \left\{ {\begin{array}{*{20}c} {\cfrac{{dy}}{{dt}} = f(t,y)} \\ {y(t_0 ) = y_0 } \\ \end{array} } \right.  
Donde y(t_0) = y_0\, es la condición inicial.
Entre los tipos de EDOs de primer orden se encuentran:

Ecuación de variables separables

Son EDOs de la forma:
\frac{dy}{dt} = f(t,y)
En donde es posible "despejar" todos los términos con la variable dependiente en función de la variable independiente, quedando ahora la ecuación:
\ g(y)dy=h(t)dt
En donde se procede integrando ambos miembros de la ecuación
\int g(y)dy=\int h(t)dt
De donde es posible obtener la solución

Ecuación exacta

Una ecuación de la forma:
M(x, y)\, dx + N(x, y)\, dy = 0, \,\!
se dice exacta si existe una función F que cumpla:
\frac{\partial F}{\partial x}(x, y) = M
y
\frac{\partial F}{\partial y}(x, y) = N.
Su solución es entonces:
F(x, y) = C.\,
  • Ecuación de Coeficientes Homogéneos (llamada comúnmente homogénea). 

Ecuación lineal

Una ecuación diferencial es lineal si presenta la forma:
y'+ P(x)y = Q(x)\,
Y que tienen por solución:
y(x) =e^{ - \int P(x) dx } \left( C + \int Q(x) e^{ \int P(x) dx } dx \right)
Como se puede apreciar, esta ecuación es una ecuación diferencial de Bernoulli, con n=0.

Ecuación de Riccati

Una ecuación diferencial tiene la forma de la introducida por Jacobo Francesco Riccati cuando presenta la estructura:
y'(x) + P(x)y^2 + Q(x)y + R(x)=0\,
Para resolverla, se debe hacer la sustitución y=y_{p}+ \frac{1}{z}, donde yp es una solución particular cualquiera de la ecuación.

Ecuación de Lagrange


Una ecuación diferencial de Lagrange presenta la forma:
y=g(y')x + f(y')\,
Resolviéndose con la sustitución y' = p, obteniéndose una solución general y una solución particular.

Ecuación de Clairaut

Una ecuación diferencial de Clairaut, llamada así en honor a Alexis-Claude Clairaut,tiene la forma:
y= xy' + f(y')\,
Como se puede apreciar, esta ecuación es una forma particular de la ecuación diferencial de Lagrange, con g(y') = y', por lo cual, su resolución es análoga a la anterior.



 

Publicado por en