Bienvenidos

BIENVENIDOS A MI BLOG

funcion homogenea. ecuacion diferencial homogenea. resolucion de ecuaciones diferenciales reducibles a homogeneas.

                                   Función homogénea

una función homogénea es una función que presenta un comportamiento multiplicativo de escala interesante: si todos los argumentos se multiplican por un factor constante, entonces el valor de la función resulta ser un cierto número de veces el factor multiplicativo elevado a una potencia. Dicha potencia es el grado de la función homogéne.

ejemplo:
  1. La función $f(x,y)= \frac{1}{\sqrt{x+y}}$ es homogéénea de grado $\frac{1}{2}$.
  2. Las funciones $f(x,y)=e{\frac{x}{y} }$, $f(x,y)= \frac{x^2 - y^2}{x^2 + y^2} $, $f(x,y)=\frac{x}{2x+y}$ son homogéneas de grado 0.
  3. Las funciones $f(x,y)= x^2 + y^2$, $f(x,y)=xy$, $f(x,y)=x^2-2xy+y^2$ son homogéneas de grado 2.
Ahora definimos lo que es una ecuación diferencial homogén.


                                 Ecuacion diferencial homogenea

Existen algunas ecuaciones diferenciales que al hacer un cambio de variable adecuado se reducen a ecuaciones en variables separadas, como el ejemplo anterior.
Antes de estudiar las ecuaciones diferenciales homogéneas es necesario definir lo que es una función homogénea.
 
Una ecuación diferencial ordinaria de primer orden, $y^{\prime} = f(x,y)$, es homogénea si la función $f(x,y)$ es homogénea de orden cero.
 
Observación: si la ecuación diferencial está escrita en la forma
\begin{displaymath} M(x,y) dx + N(x,y) dy = 0 \end{displaymath}

sería homogénea sí y sólo sí los coeficientes $M(x,y)$ y $N(x,y)$ son funciones homogéneos del mismo grado. 

ejercicios:

Convertir el problema:

ejercicios resueltos

en un problema de condiciones de contorno homogéneas.
Nos conviene construir una función v(x, t) que satisfaga al menos las dos condiciones de contorno dadas, v(o, t) = sen2 t ; v(1, t) = 0. Fácilmente vemos que esa función puede ser :

ejercicios resueltos

tomamos entonces:

ejercicios resueltos 

con lo que la ecuación diferencial y las condiciones se transforman como sigue :

ejercicios resueltos  
Sustituyendo estos valores obtenemos:

ejercicios resueltos  
Una vez obtenida la solución para w(x,t), la función original vendrá dada por:

ejercicios resueltos

El método para obtener w(x,t) es análogo al de otros casos de ecuaciones no homogéneas.
 

    Resolucion de Ecuaciones diferenciales reducibles a    homogeneas: 
Son aquellas que mediante un cambio de variable se convierten en homogéneas.

EJEMPLOS DE ECUACIONES DIFERENCIALES REDUCIBLES A HOMOGÉNEAS
Ejemplo 1.- Resolver la ecuación diferencial:

ecuaciones diferenciales

Podemos aplicar el método de resolución de ecuaciones diferenciales homogéneas puesto que P y Q son funciones homogéneas de grado 3. Haciendo el cambio v = y/x tenemos:

ecuaciones diferenciales

Y separando variables para integrar:

ecuaciones diferenciales

Que después de deshacer el cambio queda en la forma:

ecuaciones diferenciales

La ecuación puede tener soluciones singulares que vienen dadas por:

ecuaciones diferenciales

El caso x = 0 es una solución incluida en la general, ya que basta sustituir x por 0 en la ecuación diferencial para ver que esta se hace idénticamente nula. Para el otro caso tenemos:

ecuaciones diferenciales

Que es una solución singular no incluida en la general.


ECUACIONES DIFERENCIALES REDUCIBLES A HOMOGÉNEAS
Las ecuaciones diferenciales de la forma:

ecuaciones diferenciales

Son homogéneas si se tiene c1 = c2 = 0.

Cuando se tiene , la anterior ecuación puede transformarse en homogénea mediante una traslación de ejes, es decir, poniendo x = X + h ; y = Y + k, donde h y k vienen dados por el sistema:

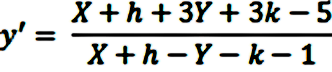
ecuaciones diferenciales

Si este sistema no es compatible, siempre podemos poner:

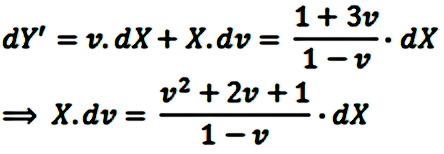
ecuaciones diferenciales

Con lo que obtenemos:

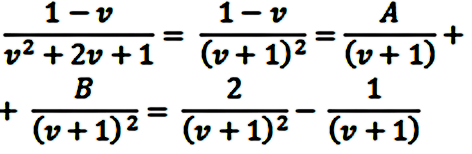
ecuaciones diferenciales

Y haciendo el cambio:

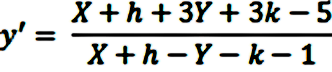
ecuaciones diferenciales

Con lo que sustituyendo:

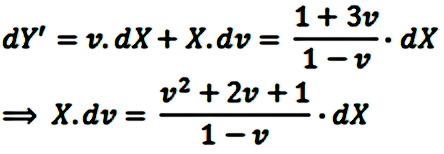
ecuaciones diferenciales

Que es una ecuación en variables separadas cuya solución viene dada por:

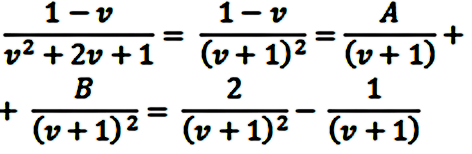
ecuaciones diferenciales

Ejemplo.- Resolver la ecuación diferencial:

ecuaciones diferenciales

Para convertir esta ecuación diferencial en homogénea hacemos el cambio sugerido en la parte de teoría, con lo que resulta:

ecuaciones diferenciales

Y para que sea homogénea se ha de cumplir:

ecuaciones diferenciales

Según esto nos queda:

ecuaciones diferenciales

Y haciendo el cambio v = Y/X, obtenemos:

ecuaciones diferenciales

Y separando variables:

ecuaciones diferenciales

Para resolver la primera integral aplicamos el método de fracciones simples:

ecuaciones diferenciales

Con lo que tenemos:

ecuaciones diferenciales

Y deshaciendo el cambio:

ecuaciones diferenciales

Ecuación que también podemos poner:

ecuaciones diferenciales




      



Publicado por en