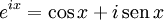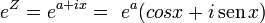formula de Euler y Teorema de Moivre.

                                     Fórmula de Eule

La fórmula o relación de Euler, atribuida a Leonhard Euler, establece que:

para todo número real x. Aquí, e es la base del logaritmo natural, i es la unidad imaginaria y senx y cosx son funciones trigonométricas.
Ó bien:

siendo Z la variable compleja formada por : Z=a+ix.

DEMOSTRACIÓN DE LA FÓRMULA DE EULER

Partiendo de las Series de Taylor (1), (2) y (3):

   

    

    

  

  

Si en (1) sustituimos  x  por  z·i,
Si consideramos que  i¹ = i,   i² = -1,   i³ = -i,   i⁴ = 1,   etc.
Si agrupamos las potencias pares de z por un lado y las impares por otro, entonces:

Sustituyendo (2)  y  (3) tenemos:

Sustituyendo z por π (PI)  

Por lo tanto, obtenemos la Identidad de Euler / Lindeman:

e^{i · π} + 1 = 0

                                   Teorema de Moivre

Fórmula para calcular las potencias zⁿ de un número complejo z. El teorema de De Moivre establece que si un número complejo z = r(cos x + i sin x), entonces zⁿ = rⁿ(cos nx + i sin nx), en donde n puede ser enteros positivos, enteros negativos, y exponentes fraccionarios.

La fórmula de De Moivre puede ser obtenida de la fórmula de Euler:

aplicando leyes de la exponenciación

  

Entonces, por la fórmula de Euler,