Funciones de Variable Compleja
z = z1 + iz2
Es una serie de operaciones que se hacen a una variable y de las que se obtiene un valor. Cuando la variable es un número complejo, a la función se llama función de variable compleja. Podemos imaginarnos la función como una máquina a la que se le suministra unos datos y que obtiene un valor.
Ejemplo: Sea la función w = Az, en el que A es una constante compleja y z una variable compleja. Expresando A y z en la forma exponencial:
A = a eia
z = r eib Entonces w = ar ei(a + b)
Si dibujamos en un plano varios puntos (serían los puntos z) y en otro plano los puntos w obtenidos al aplicar la función, veremos que la distancia de los puntos z al origen de coordenadas ha sido aumentada o disminuido por el factor a y girados al rededor del origen un ángulo a.
Sea la función w = z + A.
Expresando A y z en forma binaria:
A = a1 + ia2z = z1 + iz2
Entonces w = (a1 + z1) + i(a2 + z2)
Si dibujamos en un plano varios puntos (serían los puntos z) y en otro plano los puntos w obtenidos al aplicar la función, veremos que los puntos z han sido desplazados según el vector A.
Sea la función w = 1/z .
Cuando aplicamos esta función a la recta x = c obtenemos la circunferencia
(u - 1/2c)2 + v2 = (1/2c)2.
Cuando aplicamos esta función a la recta y = c obtenemos la circunferencia (v - 1/2c)2 + u2 = (1/2c)2.
Si aplicamos la función w = 1/z a las circunferencias anteriores obtendremos las rectas correspondientes.
De la recta real al plano complejo
La idea de función de variable (o variables) reales puede ser extendida (continuada, le dicen también) al Plano complejo. La idea es la de siempre: si en una determinada región del plano complejo R a un número complejo z le corresponde un numero (o varios números) complejos w = f(z), diremos que f(z) es una función de variable compleja z. Obvio que f(z) puede ser biyectiva, en cuyo caso tendremos que a z le estará asociado uno y solo un numero complejo w = f(z). Es claro también que siempre se podrá expresar f(z) = u(x, y) + iv(x, y) con u(x, y) la parte real y v(x, y) la parte imaginaria (1), Esta representación tiene una interpretación adicional. Como representamos un numero complejo en el plano 0xy como z = x + iy, pero w = f(z) también podrá ser representada como un punto en el plano 0uv.
Entonces, desde el punto de vista geométrico una función de variable compleja podrá ser entendida como una ley de transformación entre pares de puntos (x, y) del plano 0xy del argumento z y los puntos (u, v) del plano 0uv de valor w.
Continuidad en el plano complejo
Podemos también extender el concepto de continuidad de una función de variable real a una función de variable compleja. Esto es: diremos que una función compleja1 w = f(z) será continua en z0 si para un 1A partir de ahora y por razones de simplicidad llamaremos a f(z) función compleja en vez de función de variable compleja.
ejemplo:
Vamos a estudiar la función  sobre el circuito adjunto con lo que tendremos :
sobre el circuito adjunto con lo que tendremos :


y la integral es nula por no haber ningún polo de f(z) en el circuito. Continuando resulta:

Y tenemos: en BC.- z = R+i.y , con O < y < a , dz = i.dy :
Y la última expresión tiende a cero cuando R tiende a infinito. Aná1ogamente resulta para la última de las integrales, con lo que nos queda, para la tercera : en CD.- z = x + i.a , x en el intervalo (R,-R) :
Y la última expresión tiende a cero cuando R tiende a infinito. Aná1ogamente resulta para la última de las integrales, con lo que nos queda, para la tercera : en CD.- z = x + i.a , x en el intervalo (R,-R) :
De ese modo, finalmente :

siendo la integral  una que aparece en el estudio de la función Gamma de Euler. Por otro lado , para la función de variable real que estamos estudiando, tenemos :
una que aparece en el estudio de la función Gamma de Euler. Por otro lado , para la función de variable real que estamos estudiando, tenemos :

Pero el primer integrando es una función par que nos permite continuar la igualdad en la forma :

con lo que finalmente resulta :
con lo que finalmente resulta :
ejemplo:
Resolver las integrales de Fresnel :
Tomaremos como función a estudiar  , y como circuito el representado en la figura adjunta. Aplicando el teorema de los residuos, y considerando que no hay ningún cero en el recinto, tenemos :
, y como circuito el representado en la figura adjunta. Aplicando el teorema de los residuos, y considerando que no hay ningún cero en el recinto, tenemos :



Para la segunda integral tenemos :


Y esto resulta de que en AB :


Nos queda calcular la última de las integrales, para la que tenemos:


En consecuencia :

onde nos aparece la integral de Euler, vista en otros problemas. Continuando nos queda :


ejercicios propuestos:
Se demuestra en teoría que si una función es análitica, la suma de todos sus residuos, comprendido el del infinito, es cero. Aplicar lo dicho al cálculo de la integral :

Ejercicio:
Sea f(z) una función análitica en un dominio D, y sea C el contorno de dicho dominio. Si z1,… , zk son polos exteriores, se demuestra que podemos escribir:

donde el símbolo indica que la integral se hace en sentido negativo. Teniendo en cuenta lo anterior podemos escribir :
indica que la integral se hace en sentido negativo. Teniendo en cuenta lo anterior podemos escribir :

y tenemos :
donde el símbolo

y tenemos :
Si z =es cero de primer orden, entonces : Res(f,
) = -Lím z.f(z) (cuando z
)
Si z =es cero de orden > , entonces : Res(f,
) = 0
Si z =es polo de orden n, entonces : Res(f,
) = - Res[(1/z2 ).f(z) , 0]
Como aplicación a estos conceptos calcúlese la integral :

Definición de transformación lineal
Se denomina transformación lineal, función lineal o aplicación lineal a toda aplicación cuyo dominio y codominio sean espacios vectoriales y se cumplan las siguientes condiciones:
Transformación lineal: Sean V y W espacios vectoriales reales. Una transformación lineal T de V en W es una función que asigna a cada vector v ϵ V un vector único Tv ϵ W y que satisface, para cada u y v en V y cada escalar ∝,
- T (u+v)= Tu+Tv
- T(∝v)= ∝Tv, donde ∝ es un escalar.
Ejemplos propuestos:
1. Sea T: R2 → R2 definida por T(x, y) = (x + y, y). Determina si T es una transformación lineal.
2. Sea T: R2 → R2 definida por T(x, y) = (-x , y). Esto es, T(1, 2) = (-1, 2). Determina si T es una transformación lineal.
3. La función f: R → R definida por f(x) = x2 no es una transformación lineal, pues, (x + y)2 ≠ x2 + y2. En particular, 5 = 2 + 3 pero:
f(5) = 52 = 25 ≠ 13 = 22 + 32 = f(2) + f(3).
ejercicios resueltos:

es una transformación lineal.
Veamos primero que  respeta la suma.
respeta la suma.
1Sean cualesquiera en
cualesquiera en 
T((x;y)+(x';y')) = T((x+x';y+y'))
= (y+y';x+x')
= (y;x)+(y';x')
= T((x;y))+T((x';y'))
Ahora la multiplicación por escalar.
Sea cualesquiera en
cualesquiera en  y
y  en
en 
T(a(x;y)) = T((ax;ay))
= (ay;ax)
= a(y;x)
= aT((x;y))
con lo cual hemos demostrado que es una transformación lineal.
es una transformación lineal.
 respeta la suma.
respeta la suma. 1Sean
 cualesquiera en
cualesquiera en 
T((x;y)+(x';y')) = T((x+x';y+y'))
= (y+y';x+x')
= (y;x)+(y';x')
= T((x;y))+T((x';y'))
Ahora la multiplicación por escalar.
Sea
 cualesquiera en
cualesquiera en  y
y  en
en 
T(a(x;y)) = T((ax;ay))
= (ay;ax)
= a(y;x)
= aT((x;y))
con lo cual hemos demostrado que
 es una transformación lineal.
es una transformación lineal.2.Demostrar que la siguiente función

es una transformación lineal.
Solución: Veamos primero que respeta la suma.
respeta la suma.
Sean cualesquiera en
cualesquiera en 
T((x;y)+(x';y')) = T((x+x';y+y'))
= (2(x+x')+3(y+y');(x+x')-3(y+y'))
= (2x+2x'+3y+3y';x+x'-3y-3y')
= (2x+3y;x-3y')+(2x'+3y';x'-3y')
= T((x;y))+T((x';y'))
Ahora la multiplicación por escalar.
Sea cualesquiera en
cualesquiera en  y
y  en
en 
T(a(x;y)) = T((ax;ay))
= (2ax+3ay;ax-3ay)
= (a(2x+3y);a(x-3y))
= a(2x+3y;x-3y)
= aT((x;y))
con lo cual hemos demostrado que es una transformación lineal.
es una transformación lineal.
Solución: Veamos primero que
 respeta la suma.
respeta la suma. Sean
 cualesquiera en
cualesquiera en 
T((x;y)+(x';y')) = T((x+x';y+y'))
= (2(x+x')+3(y+y');(x+x')-3(y+y'))
= (2x+2x'+3y+3y';x+x'-3y-3y')
= (2x+3y;x-3y')+(2x'+3y';x'-3y')
= T((x;y))+T((x';y'))
Ahora la multiplicación por escalar.
Sea
 cualesquiera en
cualesquiera en  y
y  en
en 
T(a(x;y)) = T((ax;ay))
= (2ax+3ay;ax-3ay)
= (a(2x+3y);a(x-3y))
= a(2x+3y;x-3y)
= aT((x;y))
con lo cual hemos demostrado que
 es una transformación lineal.
es una transformación lineal.Formas Cartesiana y Polar
En coordenadas polar
El sistema de coordenadas polares es un sistema de coordenadas bidimensional en el cual cada punto o posición del plano se determina por un ángulo y una distancia.
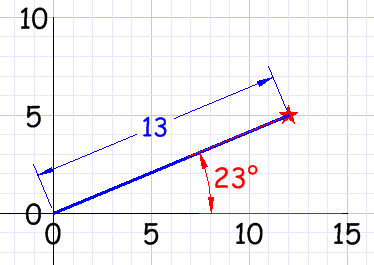
Coordenadas polares
Con coordenadas polares señalas un punto diciendo la distancia y el ángulo que se forma:
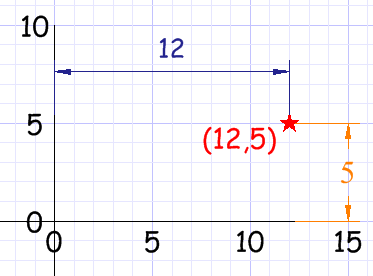
Coordenadas cartesianas
Con coordenadas cartesianas señalas un punto diciendo la distancia de lado y la distancia vertical:
Ejemplos:
Conversión de coordenadas polares a cartesianas

x = r · cos α
y = r · sen α
Ejemplos
2120º


10º = (1, 0)
1180º = (−1, 0)
190º = (0, 1)
1270º = −(0, −1)
Conversión de coordenadas cartesianas a polares

2120º
2240º
2300º
(2, 0)
20º
(−2, 0)
2180º
(0, 2)
290º
(0, −2)
