Condiciones de Cauchy-Riemann
Las condiciones de Cauchy-Riemann son básicas en el Análisis Complejo, debido a que su verificación constituye una condición necesaria para la derivabilidad de este tipo de funciones.
Sea una función compleja f(z), con z = x + iy y f(z) se puede descomponer en suma de dos funciones reales de dos variables u y v, de manera que f(z) = f(x,y) = f(x + iy) = u(x,y) + iv(x,y). Si la función f(z) sea derivable en un punto z0 = x0 + iy0 entonces deben verificarse las condiciones de Cauchy-Riemann:
Además se cumple que el valor de la derivada en el punto, de existir, debe ser:
f'(z0) = ux'(x0,y0) + ivx'(x0,y0) = vy'(x0,y0) − iuy'(x0,y0)
Existen formas equivalentes de expresar las condiciones de Cauchy-Riemann: fx + ify = 0
Las ecuaciones de Cauchy-Riemann son condición necesaria, pero no son condición suficiente para demostrar la derivabilidad de una función en un punto.
Sin embargo, existen condiciones suficientes de derivabilidad si la función, además de cumplir las ecuaciones de Cauchy-Riemann, se puede descomponer en dos funciones u y v con derivadas parciales primeras continuas en un entorno de z0 = (x0,y0).
Ejemplo resuelto:
Veamos un ejemplo donde derivable en todo número complejo y por lo tanto las ecuaciones de Cauchy-Riemann se verificarán en cualquier z = x + iy. Consideramos la función f(z) = z2. Ahora veamos esta función en coordenadas cartesianas.
f(x + yi) = (x + yi)2 = (x2 − y2) + i2xy
por lo tanto las parte real e imaginaria de la función son u(x,y) = x2 − y2 y v(x,y) = 2xy respectivamente. Derivado con respecto a x e y es inmediato que
ux = 2x = vy
y que
uy = − 2y = − vx.
Por último verifiquemos la condición sobre las derivadas. La derivada de f es claramente f'(z) = 2z (las reglas para derivar funciones complejas es similar a las funciones reales) por lo tanto
f'(x + iy) = 2(x + iy) = 2x + i2y = ux + ivx = vy − iuy
Fórmula integral de Cauchy
Cauchy fue pionero en el análisis matemático y la teoría de grupos de permutaciones, contribuyendo de manera medular a su desarrollo. También investigó la convergencia y la divergencia de las series infinitas, ecuaciones diferenciales, determinantes, probabilidad y física matemática.
Enunciado 1
Sea f(z) una función analítica en un dominio simplemente conexo D. Entonces para cualquier punto 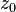 contenido en el interior de D y para cualquier camino C cerrado simple que contenga al punto se tiene
contenido en el interior de D y para cualquier camino C cerrado simple que contenga al punto se tiene
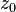 contenido en el interior de D y para cualquier camino C cerrado simple que contenga al punto se tiene
contenido en el interior de D y para cualquier camino C cerrado simple que contenga al punto se tiene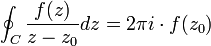
k = n + 1.kordenpolodevalorz = z0
donde la integración está tomada en sentido antihorario.
Enunciado 2
Sea  una función holomorfa (función analítica) sobre γ, γ un camino (una curva diferenciable con continuidad a trozos) cerrado y
una función holomorfa (función analítica) sobre γ, γ un camino (una curva diferenciable con continuidad a trozos) cerrado y
 una función holomorfa (función analítica) sobre γ, γ un camino (una curva diferenciable con continuidad a trozos) cerrado y
una función holomorfa (función analítica) sobre γ, γ un camino (una curva diferenciable con continuidad a trozos) cerrado y

Siendo
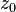 un punto,
un punto,  el índice del punto respecto a la curva (el número de veces que la curva rodea al punto teniendo en cuenta el sentido con que lo hace).
el índice del punto respecto a la curva (el número de veces que la curva rodea al punto teniendo en cuenta el sentido con que lo hace).y ademas me piden hacerlas solo con la fórmula integral de Cauchy, la ultima la hice pero no se si este buena me dio  .
.
 .
.Función armónica conjugada
función armónica es una función dos veces continuamente derivable f : D → R (donde D es un subconjunto abierto de Rn) que cumple la ecuación de Laplace, i.e.
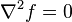 o también como
o también como 
- Ejemplos
Ejemplos de funciones armónicas de dos variables
- La parte real e imaginaria de cualquier función holomorfa
- f(x1, x2) = ln(x12 + x22)
- definida en R2 \ {0} (asi como los ies por ejemplo el potencial eléctrico debido a una carga en línea, y el potencial gravitatorio debido a una masa cilíndrica)
- Si u es una función armónica y le aplicamos una transformación conforme del plano, continúa siendo armónicA.
Ejemplos de funciones armónicas de n variables
- Las funciones afines, en particular la función constante.
- La función
 siempre que
siempre que  .
.
Propiedades de las funciones armónicas conjugada
Algunas propiedades importantes de las funciones armónicas se pueden deducir de la ecuación de Laplace.
El teorema de regularidad para las funciones armónicas
Las funciones armónicas son infinitamente derivables. De hecho, son funciones analíticas.El principio del máximo
Las funciones armónicas satisfacen el siguiente principio del máximo (conocido como el principio débil del máximo): si K es cualquier subconjunto compacto de D, entonces f, en K, alcanza sus máximo y mínimo en la frontera de K.Si además D es conexo, se tiene que f no puede tener máximos o mínimos locales, excepto si f es constante (conocido como el principio fuerte del máximo).
Integral de línea
es aquella integral cuya función es evaluada sobre una curva. En el caso de una curva es cerrada en dos dimensiones o del plano complejo, se llama también integral de contorno.Ejemplos prácticos:
- el cálculo de la longitud de una curva en el espacio,
- el cálculo del volumen de un objeto descrito por una curva, objeto del que se posee una función (campo escalar) que describe su volumen a lo largo de la curva,
- o también para el cálculo del trabajo que se realiza para mover algún objeto a lo largo de una trayectoria teniendo en cuenta campos de fuerzas (descritos por campos vectoriales) que actúen sobre el mismo.
ejemplo:
Un hombre de 160 libras lleva una cubeta de pintura de 25 libras a lo alto de un tanque a traves de una escalera helicoidal. La escalera tiene 20 pies de radio. Al alcanzar la altura máxima de 90 pies del tanque la escalera ha dado tres vueltas completas. Calcule el trabajo realizado para llevar la cubeta hasta lo más alto del tanque.
Aplicacion De La Integral De Linea Al Calculo Del Trabajo
El trabajo en la física elemental se define como “trabajo es igual a fuerza por distancia”, es decir que el trabajo que se efectúa sobre el cuerpo se da por: W = Fd , donde F es una fuerza constante que actúa sobre el cuerpo y que es paralela al desplazamiento y d es la magnitud del desplazamiento.






